论文阅读
1 介绍
首先是介绍一些概念:
最近邻搜索KNN:找到与查询点最接近的前k个点。
近似最近邻搜索:在大型高维数据库中,KNN的成本会很高,此时该问题通常会被放宽为近似最近邻搜索ANNS,允许以高概率返回最接近的前k个邻点而非精确结果。
私有最近邻搜索:客户端希望获取且仅能获取最近邻搜索的结果,同时不向服务器泄露查询内容。
以往的私有最近邻搜索存在通信成本高、依赖两个非共谋服务器的安全假设等问题,本文适用单服务器。
通常情况,ANNS需要明确知晓数据库和查询点才能进行运算,如果双方不愿意泄露数据,就需要用到MPC。如果是三方,即两个服务器,复杂度可以大幅降低,但对客户端而言,这种设定的可信度不如单服务器。
USENIX2020提出的框架SANNS是该设定,但依赖通信开销较高的技术比如分布式oblivious RAM和混淆电路。
从SANNS角度出发,分析单服务器私有ANNS两个难点:(1)ANNS一种实践是将数据库划分为若干聚类,这样只需对部分距离较近的聚类进行前k个距离计算,避免全库的扫描。在MPC中,检索近邻聚类的点需要以不经意的方式,需要依赖开销昂贵的DORAM。(2)计算前k个结果需要用秘密共享或混淆电路,前者计算会导致过多的通信轮次,后者会产生大量通信量。
本文贡献:
-
设计了一种shuffle-and-reveal协议,通过高效的PIR而非DORAM来解决点检索问题。提出了对PIR结果(特殊格式的同态加密文本)进行后处理的高效方法,使其兼容后续的MPC操作;
-
提出了一种混合基元的top-k方法,优化了top-k选择过程;
-
对PIR和距离计算中使用的同态加密文本编码进行设计,能够使用更小的HE参数,缓解与同态加密噪声相关的隐私问题;
-
引入一个完全实现端到端安全ANNS框架Panther并进行实验。
2 预备知识
2.1 密码原语
(1)additive secret sharing
一个\(l\)比特(\(l\ge 2\))的值\(x\)分为\([[x]]_c,[[x]]_s\),分别表示客户端和服务器持有的部分,重构公式为\(x=[[x]]_c+[[x]]_s\space \text{mod}\space 2^l\)。
对于实数值\(\tilde x\in R\),处理方法是先按照特定精度\(f>0\)将其编码为定点值\(x=[\tilde x^{2^f}]\in[-2^{l-1},2^{l-1}]\)再进行分享。对于布尔值,\(z=[[z]]_c^B\oplus [[z]]_s^B\)。
如果不关心份额归属时,会省略下标。
(2)混淆电路Garbled circuit
用于实现布尔电路的安全两方计算,本质是混淆方以加密格式为电路的门生成真值表,这些真值表可以由评估方进行评估。
优势在于网络交互轮次固定,这对深度电路比如求最值、排序电路非常有用。
(3)Lattice-based additive homomorphic encryption
同态加密核心是明文\(x\)加密后无需解密密钥,就能直接对密文进行计算。本文采用BFV方案,适用于多项式环上的加密计算,能高效支持加法和乘法操作。
BFV的公开参数定义为\(\text{HE.pp}=\lbrace N,p,q\rbrace\):
-
\(N\)是多项式环的维度,对应多项式的最高次数(多项式形式为\(\sum_{i=0}^{N-1}a[i]x^i\)),决定了加密并行度和安全性;
-
\(q\)是密文空间的模数,定义密文所属的多项式环\(A_{N,q}\)(即系数在模\(q\)下的\(N\)次多项式集合);
-
\(p\)是明文空间的模数。
BFV的四个函数:
-
\(\text{KeyGen}\):生成加密所需的密钥对\(sk\in A_{N,q},pk\in A_{N,q}^2\);
-
\(\text{Encryption}\):用\(pk\)对明文\(\hat m\)加密生成密文,密文形式是多项式对\((\hat b,\hat a)\);
-
\(\text{Addition}\):输入加密\(\hat m_0,\hat m_1\)的密文\(ct_0,ct_1\),计算\((\hat b_0+\hat b_1\space\text{mod}\space q,\hat a_0+\hat a_1\space\text{mod}\space q)\),可以被解密为\(\hat m_0+\hat m_1\space \text{mod}\space p\);
-
常数乘法:密文与明文常数相乘,结果解密后为明文与该常数的乘积。
本文使用混合密码原语设计,优先使用基于格的同态加密,对HE不适用的场景切换为秘密分享技术。
使用\([[\vec a]]_l^H\)表示由\(P_l\)持有的密文,该密文是用\(P_{1-l}\)的公钥加密的,其中向量\(\vec a\)在加密前会被转换为多项式\(\hat a=\sum_{i=0}^{N-1}\vec a[i]X^i\)。
HE到算术秘密分享的转换(H2A):\([[\vec a]]_l^H\)转为秘密分享\([[\vec a]]\)的流程为:
-
\(P_l\)采样多项式\(\hat r\)并将和\(ct=[[\vec a]]_l^H \boxplus \hat r\)发给对方;
-
\(P_{1-l}\)解密\(ct\)得到多项式\(\hat a+\hat r\space \text{mod}\space p\),将该多项式的系数提取作为其份额\([[\vec a]]_{1-l}\);
-
\(P_l\)份额为\([[\vec a[i]]]_l=-\lceil 2^l\cdot \hat r[i]/q\rfloor \space \text{mod}\space 2^l\)。
(4)批量PIR
私有信息检索PIR是一类协议,它使客户端能使用私有索引\(i\)查询服务器数据库,从而让客户端获取\(db[i]\),同时服务器无法得知\(i\)。一种变体是客户端同时查询一组索引\(I=\lbrace i_1,i_2,\cdots,i_m\rbrace\),借助概率批量编码PBC,这种方式比进行\(m\)次独立查询更高效。
2.2 基于聚类的ANNS
ANNS方法可以归纳为基于图或树的方法、基于局部敏感哈希的方法以及基于聚类的方法。
明文场景下,HNSW为代表的基于图的方法性能最好,但其对安全计算并不友好,因为依赖无法并行执行的层次化内存操作。安全计算中基于聚类的算法效率颇高,因此本文选择基于聚类的算法作为底层明文方法。
基于聚类的ANNS流程:

大致步骤为:
-
将数据库条目划分为\(t\)个聚类;
-
选择聚类中心与查询点最接近的前\(u\)个聚类;
-
检索这\(u\)个聚类中的点;
-
从检索到的点中选择与查询点最接近的前\(k\)个点。
该算法通过排除距离较远的聚类,大幅缩减了搜索空间。
3 问题设置
3.1 威胁模型
针对静态半诚实概率多项式时间(PPT)敌手A提供两方计算安全性。考虑的是计算能力有限的敌手A,它在协议执行开始时就会腐化服务器或客户端。
3.2 基于聚类的私有ANNS综述
私有ANNS就是将算法的操作都替换为MPC版本,即距离计算(2、9行)、top-K选择(4-5、11-12行)、点检索(7)。中间结果都以秘密分享形式保存。
这三项操作,距离计算可以通过BFV完成。三项操作在总时间成本的占据大约为:10-20%,点检索超50%,topK约占30%。
Panther和SANNS的技术比较:
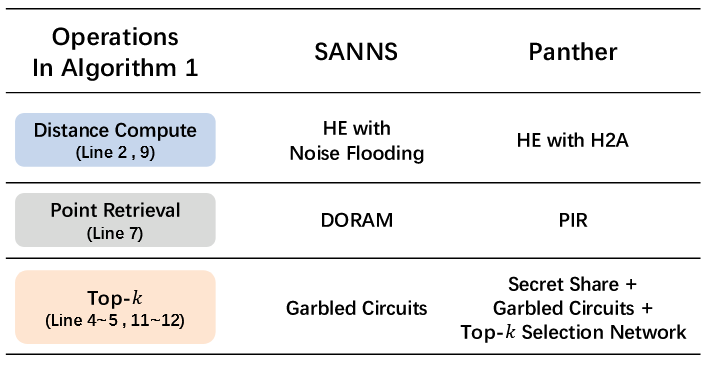
4 通过批处理PIR进行点检索
点检索由多次不经意数据库读取操作构成,其中查询ID(簇地址)以秘密共享形式存在,而数据库由服务器单独持有。SANNS的DORAM属于过度设计,因为它原本是为查询ID和数据库都是秘密分享形式的场景设计的。如果服务器知晓数据库内容,PIR更加高效,能显著降低通信开销。代价是计算开销略高,但可以通过多线程实现并行处理。
4.1 Database shuffling
PIR协议客户端\(C\)知道所检索项的索引。在安全ANNS场景下,如果\(C\)知道哪些簇被检索过,可能会泄露数据集信息,比如返回簇1和簇2,\(C\)就知道这两个簇也是接近的。为了解决该问题,必须返回top-u个最近簇的秘密共享索引。设\([[id]]\)为其中某个索引,那么\(id=[[id]]_c+[[id]]_s\space \text{mod}\space t\)。
单查询PIR中,服务器根据自身持有份额对数据库进行旋转,旋转后客户端持有的份额会转化为可直接用于标准PIR协议的真实索引。
但如果使用批处理的PIR,由于批处理PIR基于布谷鸟哈希,这与数据库旋转方法不兼容,因为很难在秘密共享值上不经意地计算布谷鸟散列。
为此提出shuffle-and-reveal方法。设数据库索引为\(ID=(id_1,id_2,\cdots,id_n)\),每次查询前,服务器\(S\)选取一个新的随机排列\(\delta:Z_n^n\rightarrow Z_n^n\)并应用在\(ID\)上,得到\(\delta(ID)=(id_1^{'},\cdots,id_n^{'})\)。然后服务器与客户端共同运行某种选择函数(比如top-k),设输出为\([[O]]=([[id_{o_1}^{'}]],\cdots,[[id_{o_k}^{'}]])\),\(S\)将其持有份额披露给\(C\),那么客户端可以重构出完整的索引集合\(O\),即获得了可直接用于后续批处理PIR查询的真实索引。
该方法的安全性证明:对于任何破坏客户端的攻击者\(A\),从\((1,2,\cdots,n )\)无放回随机采样\(P=(p_1,p_2,\cdots,p_k)\),\(A\)不能区分\(O\)和\(P\)。该引理是显然的,因为无替换的随机抽样与随机排列是一样的。
还有一个问题是PIR往往会返回额外条目,这可能影响数据库隐私性。这在ANNS中不允许,后续会说明将返回结果转为秘密共享形式,从而保护隐私。有趣的是,由于最终筛选top-k,额外返回条目反而会提高准确性。
4.2 选择shuffling友好的PIR协议
适用本文的PIR协议需要满足:既能支持高效的shuffle和编码操作,又不会泄露额外的数据库信息。有一类PIR无需预处理,且直接支持系数编码而非SIMD编码,例如SealPIR、OnionPIR、Spiral,本文最后使用SealPIR。
4.3 其他优化
数据编码:传统的数据编码将多个数据点编码到同一个多项式,shuffle时需要将多项式中的数据点位置全部重排列;新的编码方式将每个数据点编码到独立的多项式中,shuffle时只需要修改索引映射表。即对于\(d\)维向量,编码时将每个维度作为多项式的一个系数。
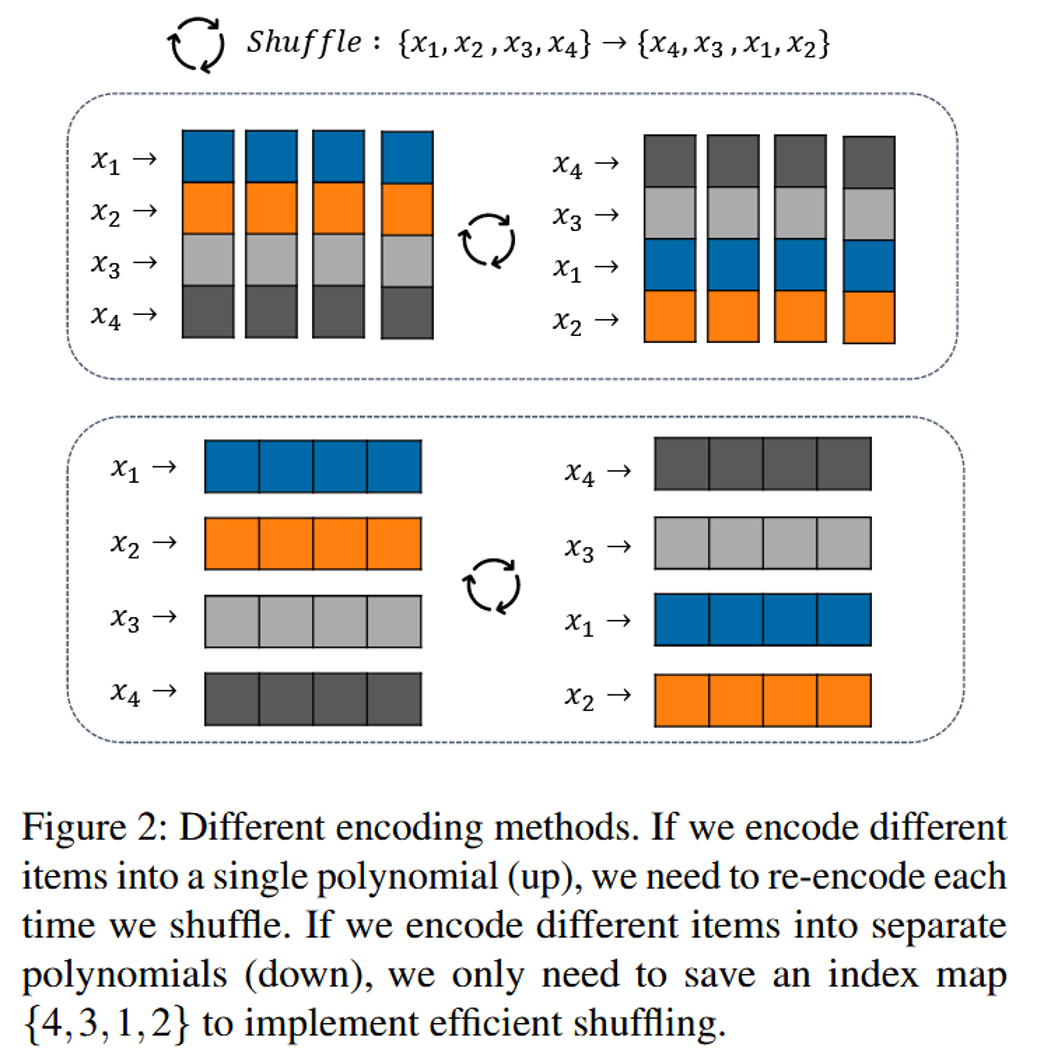
5 优化top-k
5.1 SANNS方法
top-k选择协议的性能很大程度上取决于比较协议\(\Pi_{cmp}\)的效率,而安全比较通常有GC和秘密分享两种方法可以使用。最先进的SS借助不经意传输进行比较,通信成本大幅降低,但仍需多累通信;而GC通信成本较高,但仅需恒定的通信轮数。本文使用时将充分利用两类协议的优势。
两者在两方计算中的比较:

SANNS提出的方法将比较操作的数量从\(O(nk)\)减少到\(O(n+lk)\):
-
对输入的\(n\)个条目进行洗牌,并划分为\(l\)个桶;
-
使用GC计算每个桶内的最小值;
-
使用GC计算上述\(l\)个最小值中的top-k,作为最终结果。
本文对该流程进行测试,发现第二步使用秘密分享更好,因为不同桶内的操作可以实现并行处理,且共享相同的轮次复杂度。
第二步换成秘密分享后,仅需\(O((\log l+1)\log(n/l))\)的通信轮次,通信成本为\(11nl\)比特。
5.2 更好的top-k选择
对于第三步求精确的top-k,本文使用下列算法进行优化:


但代入具体例子时,发现似乎有点问题。
6 组合
距离计算、PIR和top-k操作需要通过秘密分享的中间值连接起来,形成一个端到端的MPC应用。而Panther算法中第4、7、9行产生的输出都需要进一步处理。
首先,SealPIR 生成的密文采用 “双重加密” 格式,这给将其后续处理为秘密共享值带来了难题。其次,同态加密的密文包含噪声,这些噪声有可能泄露明文的相关信息,所以在转换为秘密共享形式之前,需要采用 “噪声淹没”(noise flooding)对策(这会增加同态加密的参数)。从效率角度考虑,近似最近邻搜索(ANNS)中的同态计算通常在相对较低的明文位宽(例如 8 位)下运行,这使得噪声淹没步骤的开销格外大。本文将进行优化,从而将所有操作无缝地链接在一起。
6.1 后处理PIR
SealPIR的双重密文无法直接H2A,因为H2A可能给第一层密文引入一位错误,破坏密文使之无法正确解密。方法是对第一层密文进行模数转换,将其从模\(q\)转为第二层密文的明文模数\(p’\)。
6.2 优化距离计算
采用的距离计算公式:\(||\vec u-\vec v||_2^2=||u||_2^2+||v||_2^2-2<\vec u,\vec v>\)
由于两方各自持有\(\vec u,\vec v\),因此两者需要协同计算的仅有内积。
假设\(P_0,P_1\)分别为客户端和服务器,\(P_0\)的查询\(\vec u=(5,4)\),\(P_1\)有两个数据\(\vec v_1=(2,7),\vec v_2=(3,6)\),那么求内积的方法是:
-
将\(\vec u\)编码为常数多项式\(\hat f\),即\(\hat f_0=5,\hat f_1=4\);
-
将\(\vec v\)编码为多项式\(\hat g_i=\sum_j \vec v_j[i]x^j\),即\(\hat g_0=2x+3x^2,\hat g_1=7x+6x^2\);
-
计算\(\hat h=\sum_i \hat f_i\hat g_i=38x+39x^2\),此时\(\hat h\)的各项系数实际上就是\(\vec u\)与\(\vec v_j\)的内积。
具体来说,\(P_0\)计算完\(\hat f\),会通过BFV加密并发送给\(P_1\),因此计算得到的\(\hat h\)也是加密的形式。\(P_1\)将\(\hat h\)发给\(P_0\),\(P_0\)解密后得到结果。
但若直接发送\(\hat h\),会让\(P_0\)有机会推断出\(P_1\)的内容,因此需要加上掩码\(\hat r\)。
SANNS的做法就是发送\(\hat h-\hat r\),让\(P_0\)解密后拿到\(\hat h-\hat r\),然后再由两方共同计算出\(\hat h\)。但这样做并不安全,因为BFV密文里有加密时故意加的噪声,这个噪声并不完全随机,而是和\(\hat f,\hat g\)有关,当\(\hat r\)是明文域的小多项式,该噪声会泄露\(\hat g\)的信息,比如大小、分布等。为了解决该问题,SANNS采用的方法是噪声淹没,往密文里加大量的额外噪声,把 “泄露信息的小噪声” 彻底淹没在 “大噪声” 里,让 \(P_0\)无法通过噪声分析出\(\hat g_i\)的信息。缺点是BFV的参数要设置成很大,性能会下降很多。
Panther的做法是使用H2A,让\(P_1\)采样密文域的随机多项式\(\hat r\),计算\(\hat h \boxplus \hat r\)发给\(P_0\),\(P_0\)用私钥解密得到\(\hat h+\hat r\)的明文,\(P_1\)根据\(\hat r\)按照之前介绍的H2A,在本地计算出自己的份额。
7 实验
数据集:SIFT(样本量1000000,维度128)、Deep1B-1M(\(n=1000000,d=96\))、Deep1B-10M(\(n=10000000,d=96\))以及 Amazon(\(n=220,d=50\))。
为确保公平性,采用与SANNS相同的超参数,比如簇的数量、近似top-k中的桶数量。
top-k评估:\(n=1000000\)个24比特的共享整数。SANNS estimation曲线是基于通信量/成本估算得出的结果。

端到端对比:
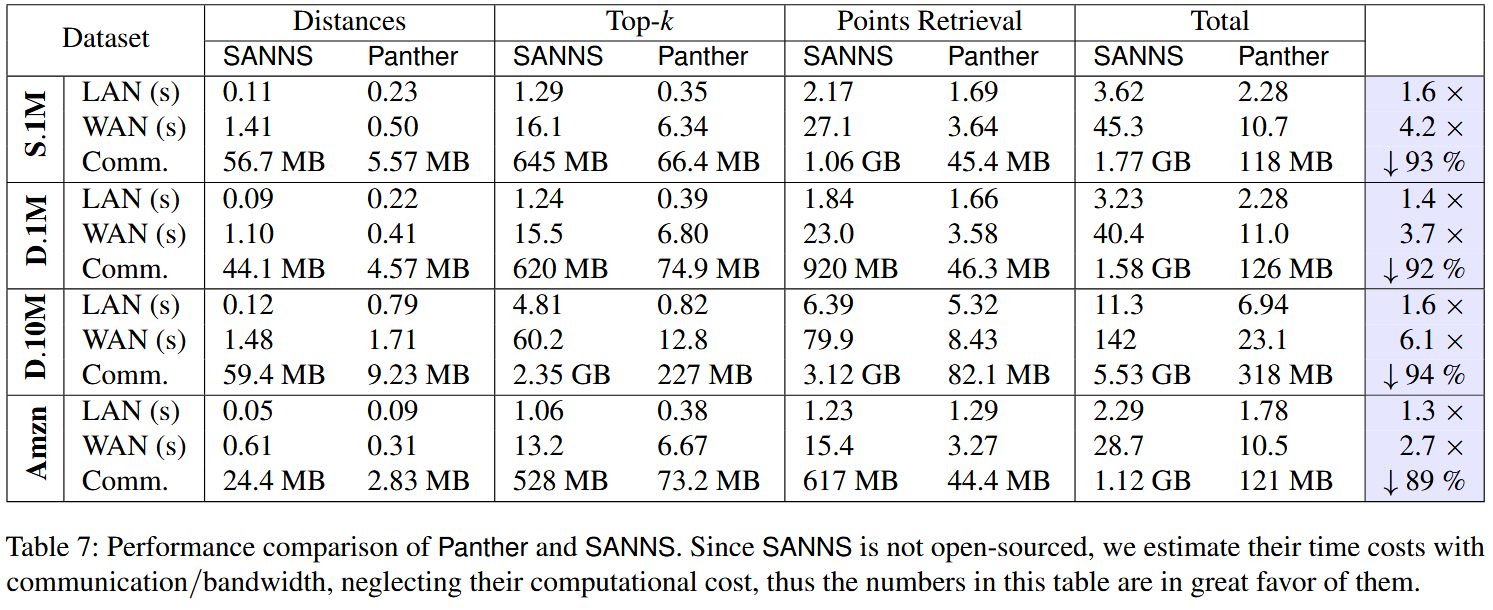
LAN估算时间慢是因为计入了CPU计算时间。
准确性:由于Panther和SANNS实现的明文流程相同,且共享同一组超参数,因此认为两者精度直接一致。