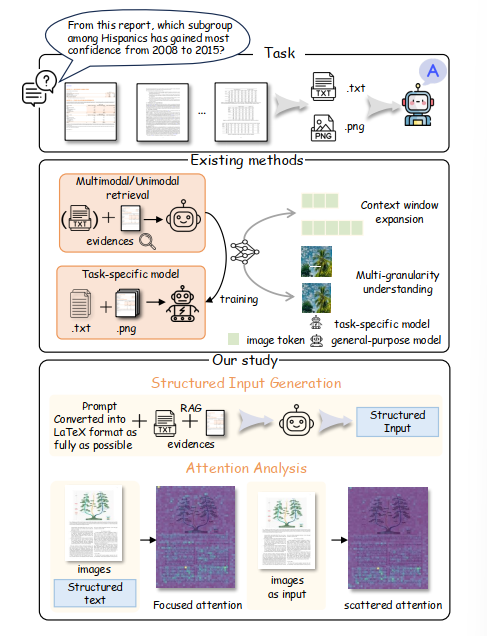
[浅谈数据结构] 浅谈树状数组

1.作用

树状数组是一种

高效

而简单的数据结构，用于*大部分

区间修改

和

查询问题

，形如\(a[1]+a[2]+a[3]+a[4]+...+a[n]\)（其不支持的可以由

线段树

替代）

2.选择原因

优点：树状数组的

码量

明显比线段树

短

，

时间复杂度

比朴素算法与线段树更

优

，

空间复杂度

则

吊打

线段树

缺点：部分线段树能解决的问题树状数组解决不了

3.基本原理&实现方法

如图(from OIWiki)

在求解\(a[1]+a[2]+a[3]+a[4]+...+a[n]\)这类问题时，根据上图这种数据结构，我们可以高效的进行查询

3.0.

lowbit

3.0.1.思路

干什么的

：求一个非负整数\(n\)表示在二进制下值为1的最低位后面的0的位数+1

怎么干

:return x&(-x)

原理

（不会可以跳过，但要背结论）:

我们得到lowbit的值，只需要得到最后一个1的位置，并且把除了这个位置之外的所有位置全部置成零。然后输出就可以。思路有了，如何操作？

根据计算机补码的性质，补码就是原码的反码加一

如：

\((110)_{2}\)

反码：

\((001)_{2}\)

加一：

\((010)_{2}\)

当反码加\(1\)后会逢\(1\)一直进位直到遇到\(0\)，这个\(0\)变成了\(1\)，操作停止。

进位的部分相当于再一次取反，也就还原原著重回0。而最后变为1的部分又停在最后一个为0的位置，也就是取反前1的位置了，正好完成操作

可以发现 没有进行操作的部分 x 与其补码即 -x 相反， 执行&操作会使没有进行操作的部分全变0，而又因为前文所述除lowbit位外其余位全部为0，&后也为0，而lowbit位lowbit前与lowbit后均相同，&后等于1，所以 x&-x 后除了 lowbit 位是1，其余位都是0，也就得到了结果

3.0.2.代码

int lowbit(int x) { return x&(-x); } 

3.1.如何修改单点？

3.1.1.思路

更新一个点也要更新其祖上十八代，祖上十八代怎么推？

我们发现每向上一层\(lowbit\)值都增加\(1\),因此得到增加单点代码：

3.1.2 代码

修改单点：

void build(int x,int k) { for(int i=x;i<=n;i+=lowbit(i)) { c[i]+=k; } } 

修改单点的扩大既是建树（只进行浅谈篇的操作）：

void build(int x,int k) { for(int i=x;i<=n;i+=lowbit(i)) { c[i]+=k; } } //... int main() { for (int i = 1; i <= n; i++) { add(i, c[i]); } } 

3.2.

如何查询1~x的和？

3.2.1.思路

举例计算\(a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]\)的和

从\(a[7]\)开始跳，跳到\(c[7]\)上，发现\(c[7]\)只管辖\(a[7]\),再跳到\(c[6]\)上，发现其管辖\(a[5]+a[6]\),再跳到\(a[4]\)上，发现其管辖\(a[1]+a[2]+a[3]+a[4]\),发现我们得到最终答案。

完整推导:

\(a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]=c[7]+c[6]+c[4]\)

关注等式右侧三个数在树上的关系

再关注等式右侧本身的关系，先推导出\(4,6,7\)的二进制表示

\(4=11_{2},6=110_{2},7=111_{2}\)

研究其关系，发现\(6=7-lowbit(7),4=6-lowbit(6)\)

所以\(code\):

3.2.2.代码

int ask(int x) { int ans=0; for(int i=1;i<=x;i-=lowbit(x)) { ans+=c[i]; } return ans; } 

3.3.如何查询任意数~x的和？

3.3.1.思路

前缀和相减（听着很抽象）

公式：\(a[1,r]-a[1,l-1]=a[l,r]\)

3.3.2.代码

int ask(int x) { int ans=0; for(int i=L-1;i;i-=lowbit(i)) { ans-=c[i]; } for(int i=R;i;i-=lowbit(i)) { ans+=c[i]; } return ans; } 

4.总结&练习&展望

4.1.总结

在浅谈篇中，注意到我们使用树状数组进行了

查询区间和

与

修改单点

的操作。这是最基本的使用。回忆一下，该二操作关键点在于\(lowbit\)。

4.2.练习

建议同学们完成:

模板：树状数组1

找逆序对

4.3.展望

在下一篇再谈篇中，我们将学习使用前缀和与差分实现区间修改与单点查询，~~~然后就可以开YNOI毒瘤了~

注意到本文由

博客园

@OIRikka,

洛谷

@March7thDev撰写，禁止

任何形式

的转载！