1. 概述
1.0. 概述
wqs 二分,即王钦石二分,是一种通过
降维
来优化 dp 的处理手段。在 OI 中,wqs 二分最常用于处理一类 2D/1D dp,常搭配斜率优化、决策单调性等其他 dp 优化方式使用,较为套路。1.1. 适用题型
wqs 二分处理的题型:
选取若干个(组)物品,数量有限制,选取有代价,询问代价极值。\(\text{eg.}\) 给定一数列 \(a_n\),要求将其按顺序分割为 \(c\) 组,使得每组的代价和最小,其中每组的代价定义为该组内所有数的和的平方。\(n,c\le10^5,a_i\ge1\)。
显然有 2D/1D 的 dp:设 \(f_{i,j}\) 为前 \(i\) 个数分了 \(j\) 组的方案,答案即为 \(f_{n,c}\),转移显然,预处理前缀和并滚掉第二维,时间复杂度 \(\mathcal{O}(cn^2)\)。斜率优化可做到 \(\mathcal{O}(cn)\),但依旧无法通过。
实际上,这大部分这一类型的题目都有类似的 2D/1D dp 的做法。
1.2. 使用前提与凸性证明
能使用 wqs 二分的前提:
记 \(f(i)\) 为选取 \(i\) 个物品时的答案,\(f\) 是凸函数,且可快速计算极值和极值点。证明函数的凸性方法很多,可以结合题目感性猜测其凸性,或是打表进行观察。
更多严谨的凸性证明见 OI Wiki,反正我看不懂 qaq。
2. 第一种理解
2.0. 核心思想
在讲算法之前,先给出它的核心思想:
- 令我们想求的值为 \(f(c)\),我们通过对 \(f\) 的解析式的处理形成一个新的函数 \(g\),使得新的函数 \(g\) 仍可快速计算极值和极值点,且其极值点恰为 \((c,g(c))\),再利用 \(f\) 和 \(g\) 的关系反推 \(f(c)\)。
听着很神奇,但先记好这个核心思想。
2.1. 算法流程
我们开始了,首先画出 \(f\) 的图像,显然它是一个离散的凸壳,接下来我们均考虑 \(f\) 下凸的情况:
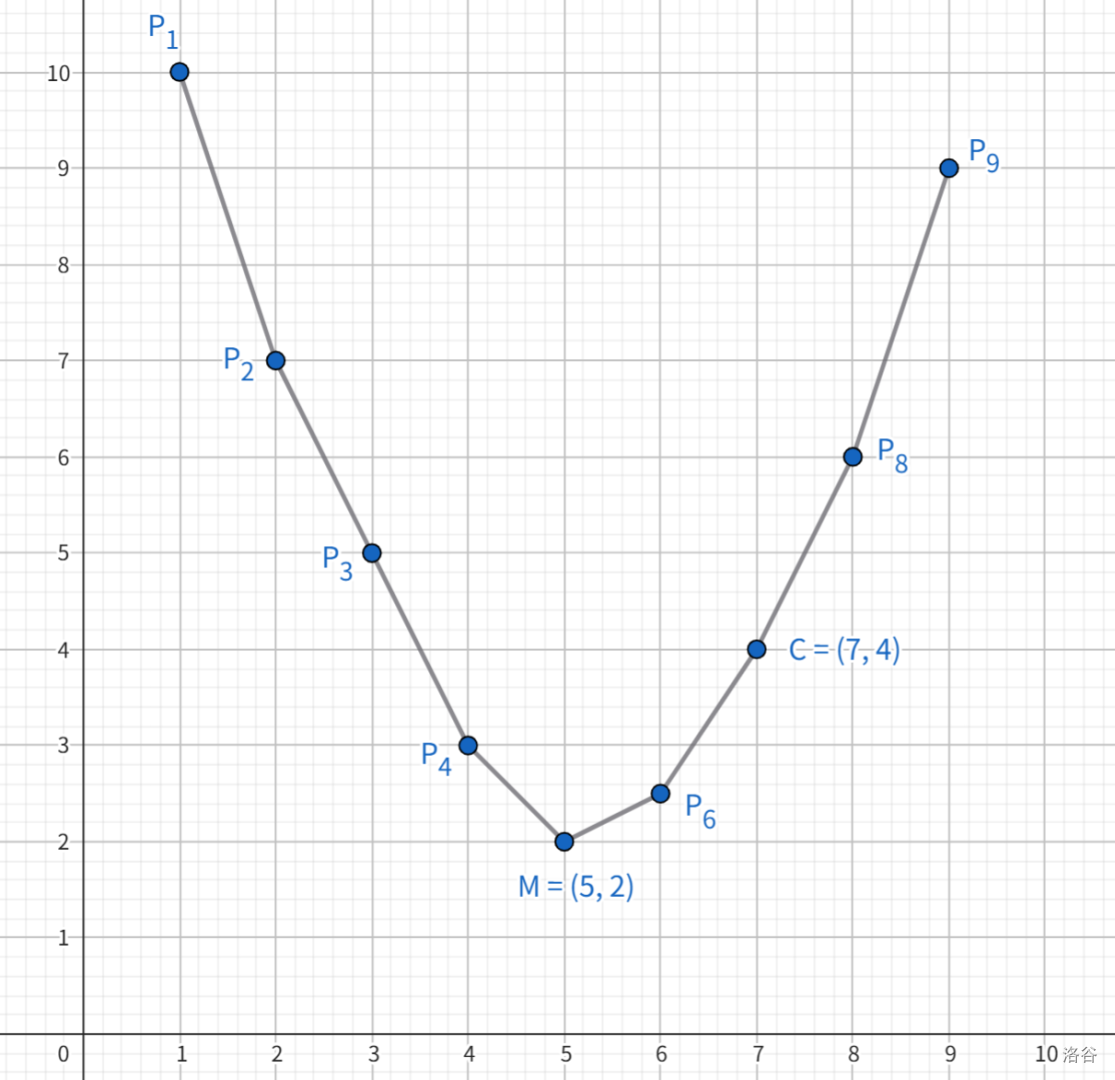
此时我们要求可以快速求出其最小值点,记此时的最小值点为 \(m\)。如图,画出 \(f\) 的导函数图像 \(f'\),\((m,f'(m))\) 与 \((m+1,f'(m+1))\) 的连线与 \(x\) 轴有交)。\(f\) 下凸,\(f'\) 是增函数。
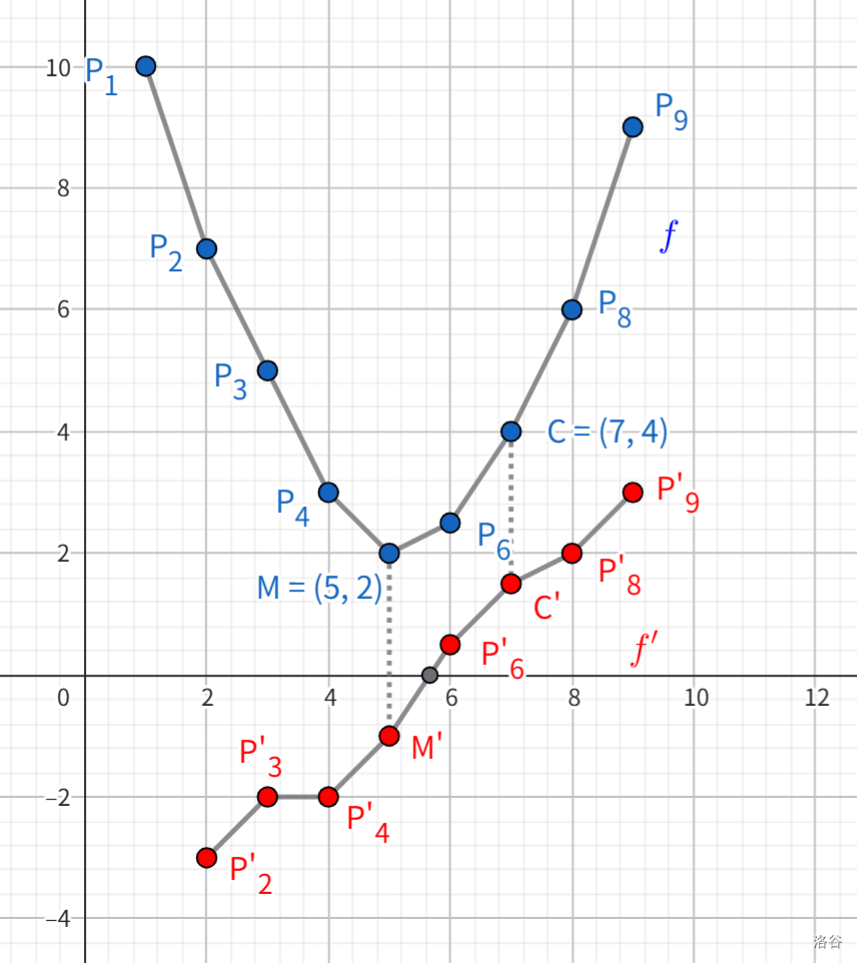
补充说明:
凸壳哪来的导数?
类比导数的定义,我们此处导数均指差分,即 \(f'(i)=\Delta_{i}=f(i)-f(i-1)\),那么此时取到最小值的点的差分为正,且它下一个数的差分为正,自己画图理解一下。但不管怎么样,肯定可以通过平移使得 \(g'(c)=0\)。二分的时候,由于我们是 dp 求极值和极值点的,所以无关紧要。
依照概述部分的核心思想,我们考虑如何构造这个 \(g\):首先我们希望最小值点落在 \(c\),怎么办呢?我们从 \(g'\) 入手。若希望最小值点落在 \(c\),需要 \((c,g'(c))\) 与 \((c+1,f'(c+1))\) 的连线与 \(x\) 轴有交,不妨令 \(g'(c)=0\)。我们让 \(f'\) 的图像在垂直方向上运动,由于它是增函数,感性理解,我们总能让它的零点落到 \(c\) 上,那这就是我们想要的 \(g'\)!
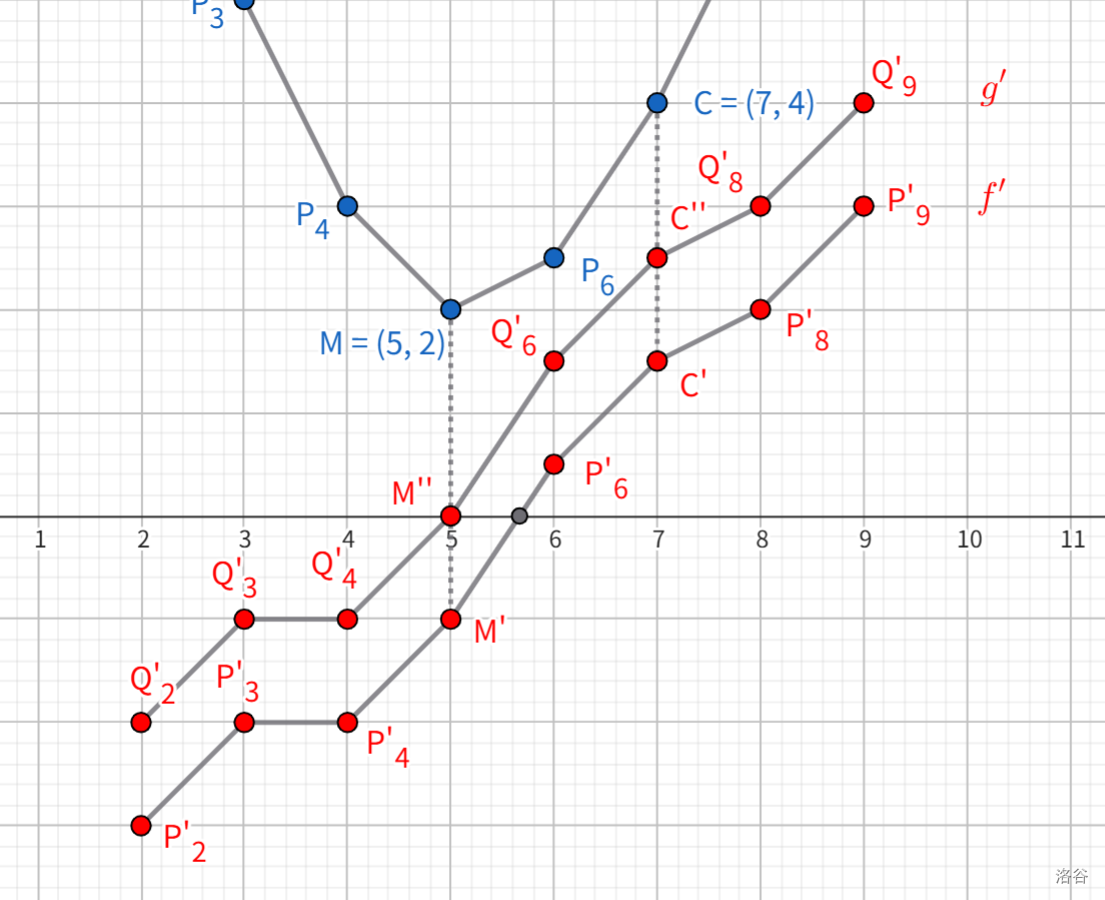
记垂直向上平移了 \(k\) 个单位长度,那么有 \(g'(i)=f'(i)+k\),容易想到 \(g(i)=f(i)+ki\) 是一个可能的构造。并且由于 \(g'\) 有 \(f'\) 平移得到,仍为增函数,所以这个 \(g\) 仍具有凸性!凸性是非常好的性质,加上 \(g(i)=f(i)+ki\) 的形式非常简单,所以一般也可同 \(f\) 一样快速计算极值和极值极值点。
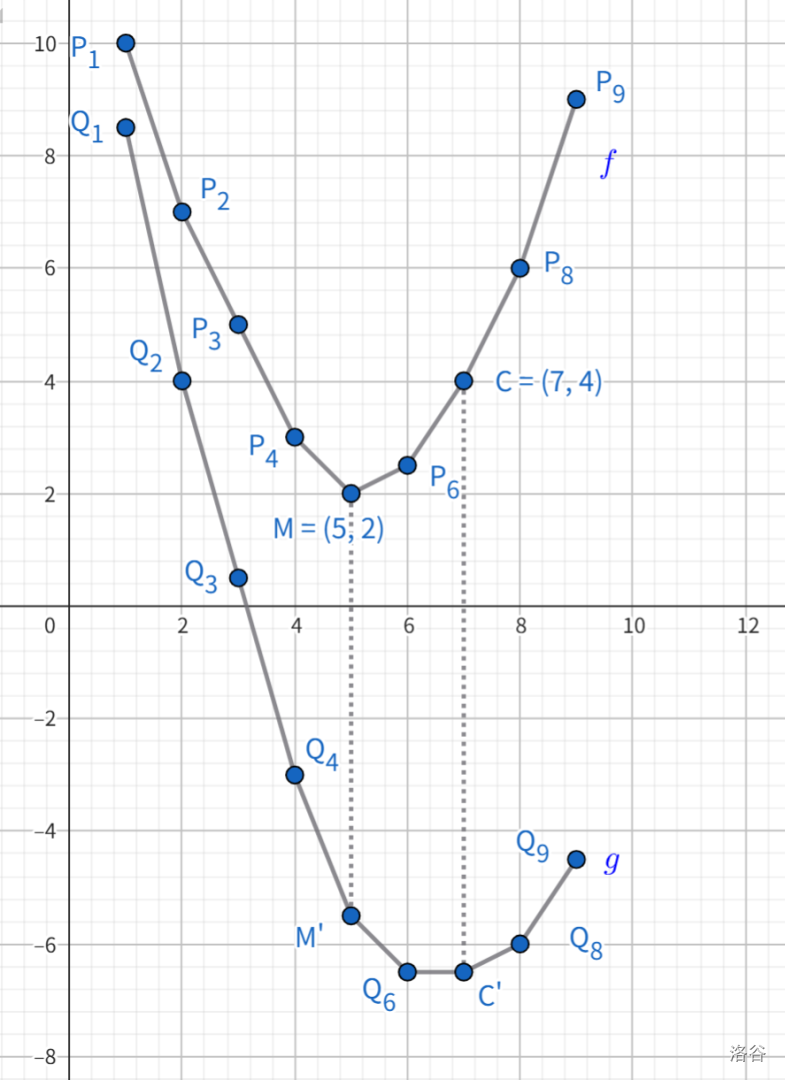
怎么完成平移的操作呢?我们二分 \(k\)。对每次二分的 \(mid\),我们求出此时 \(g\) 的极值点 \(t\):
- 若 \(t\gt c\),\(f'\) 还需向上平移,\(k\) 要增大;
- 若 \(t\lt c\),\(f'\) 还需向下平移,\(k\) 要减小。
自己对着图像理解一下。
回到 DP 部分,当我们 check 的时候,我们需求出当前 \(g\) 的最小值和最小值点,不同的是,现在不限制物品个数了!我们无需物品个数的维度,拿概述部分的例子来说:
\(\text{eg.}\) 给定一数列 \(a_n\),要求将其按顺序分割为 \(c\) 组,使得每组的代价和最小,其中每组的代价定义为该组内所有数的和的平方。\(n,c\le10^5,a_i\ge1\)。
显然有 2D/1D 的 dp:设 \(f_{i,j}\) 为前 \(i\) 个数分了 \(j\) 组的方案,答案即为 \(f_{n,c}\),转移显然,预处理前缀和并滚掉第二维,时间复杂度 \(\mathcal{O}(cn^2)\)。斜率优化可做到 \(\mathcal{O}(cn)\),但依旧无法通过。
实际上,这大部分这一类型的题目都有类似的 2D/1D dp 的做法。
容易证明它是凸的,wqs 二分可以去掉第二维,交由二分来实现。于是这个 dp 从 2D/1D 变成 1D/1D 的,我们成功实现了降维!check 里面直接写这个 dp 即可,至于极值点,转移时记录上一个状态即可。
另外,这东西本就可以斜优,所以可以做到 \(O(n\log V)\),其中 \(V\) 是二分值域。
wqs 二分就讲完了……吗?
3. 特殊情况:三点共线
考虑下图中
三点共线
的情况,那么有 \(f'(c)=f'(b)\),然后你会惊讶的发现,无论如何平移都有 \(f'(c)+k=f'(b)+k\),即 \(a,c,b\) 三点始终共线,夹在中间的 \(c\) 不可能取到最小值,怎么都二分不到!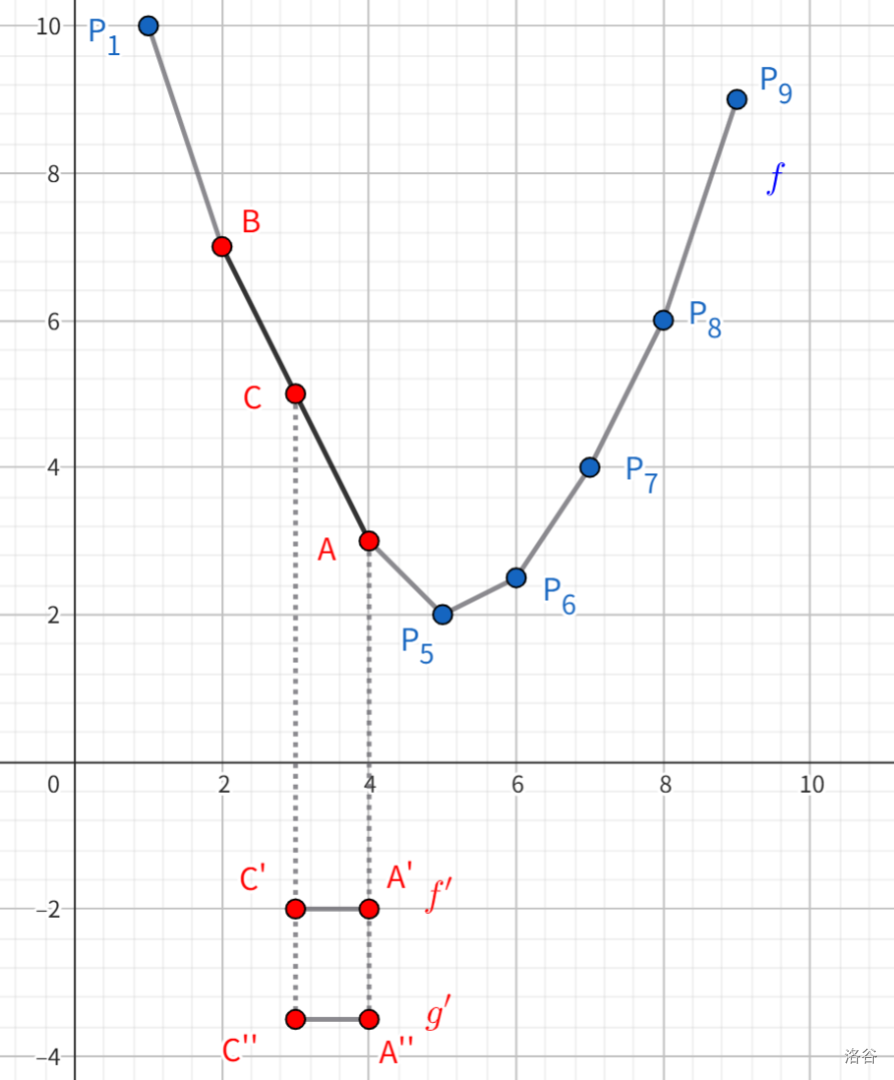
我们先二分出最小值点为 \(a\) 时的 \(g(a)\),解决方案是:\(f(c)=g(a)-kc\),为啥?先展开:
\[f(c)=g(a)-kc=f(a)+ka-kc=f(a)+k(a-c) \]即:
\[f(c)-f(a)=-k\cdot(c-a) \]这是点斜式!我们接下来只需证明 \(k_{AC}=-k\) 即可。
其实非常显然,\(f'\) 经过平移的到 \(g'\),且 \(g'(c)=0\),那么就向上平移了 \(k=-f'(c)=-k_{AC}\) 个单位长度,于是有 \(k_{AC}=-k\)。
怎么实现?找不到 \(c\) 时,我们二分出 \(c\) 右边可以取到的最接近 \(c\) 的点即可。
这个问题启发我们:\(k\) 貌似和凸壳上线段的斜率有一定联系,而我们知道凸壳上的斜率是单调的,不同斜率的直线在凸壳上的切点也是单调的,能不能利用这种性质来二分 \(k\) 呢?
所以不好意思——还没讲完。
4. 再谈算法
4.1. 第二种理解
实际上大家在网上看到的大部分博客都是这个做法,但我觉得这个做法其实比较难抓住它的动机。
依旧讨论下凸壳。
考虑一条与下凸壳相切的斜率为 \(k\) 直线 \(l_k\),记其 \(y\) 轴截距为 \(b(k)\),过凸壳上一点 \((p,f(p))\),那么有 \(f(p)=kp+b(k)\)。由凸壳相切的性质,我们必然可以找到一个 \(k\),使得与凸壳相切的 \(l_k\) 切到点 \((c,f(c))\),这时我们只需求出 \(b(k)\) 即可求出 \(f(c)\)。
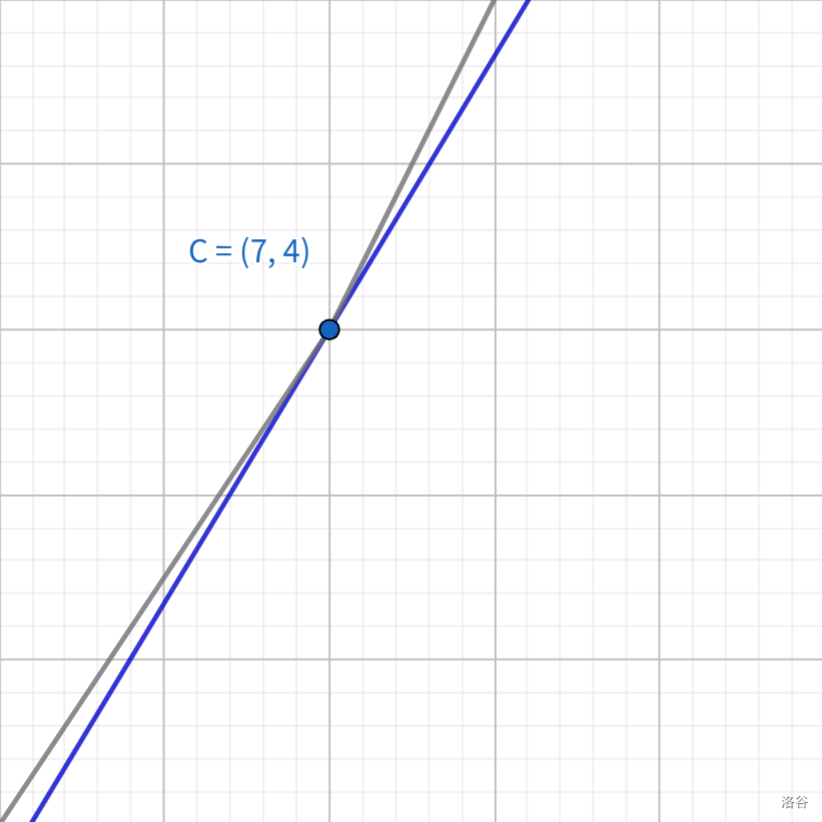
由前文所述的凸壳优秀的
切点单调性
(随斜率单调变化),我们直接二分 \(k\),好好利用这个性质来定位 \((c,f(c))\)。对于每个二分出的斜率 \(mid\),我们求出切点的横坐标 \(p\),并用其与 \(c\) 的关系判断 \(k\) 与 \(mid\) 的大小关系:- 若 \(p\lt c\),此时切点偏左,斜率偏小,\(k\gt mid\);
- 若 \(p\gt c\),此时切点偏右,斜率偏大,\(k\lt mid\)。
自己对着图像理解一下。
问题转换为求切点横坐标 \(p\)。由相切的性质,\(l\) 是所有过凸壳顶点且斜率为 \(k\) 的直线中,\(y\) 轴截距最小的。又 \(b=y-kx\),于是有 \(b(k)=\min\limits_{1\le p\le n}f(p)-kp\),且其对应的 \(p\) 即为切点横坐标。
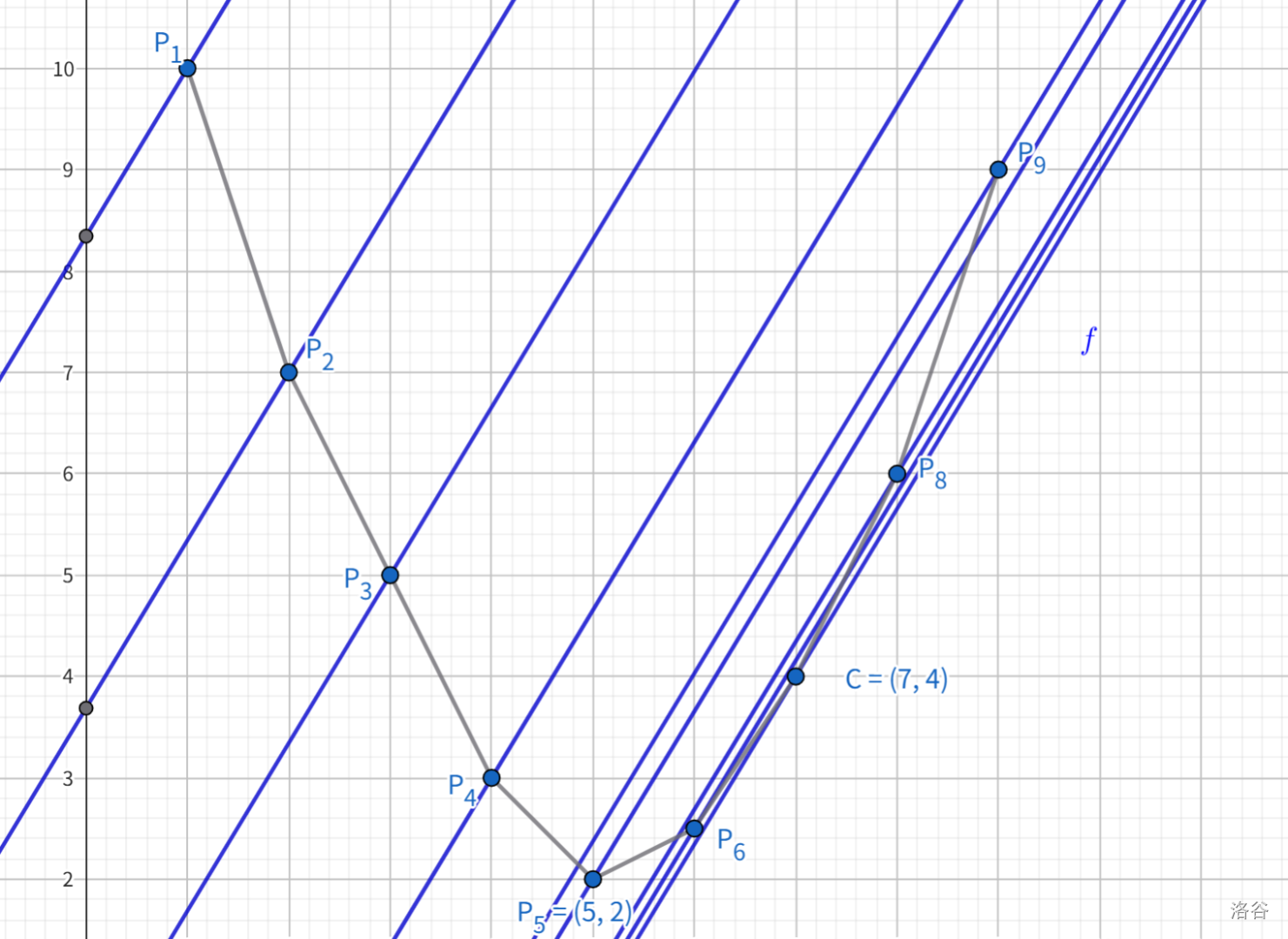
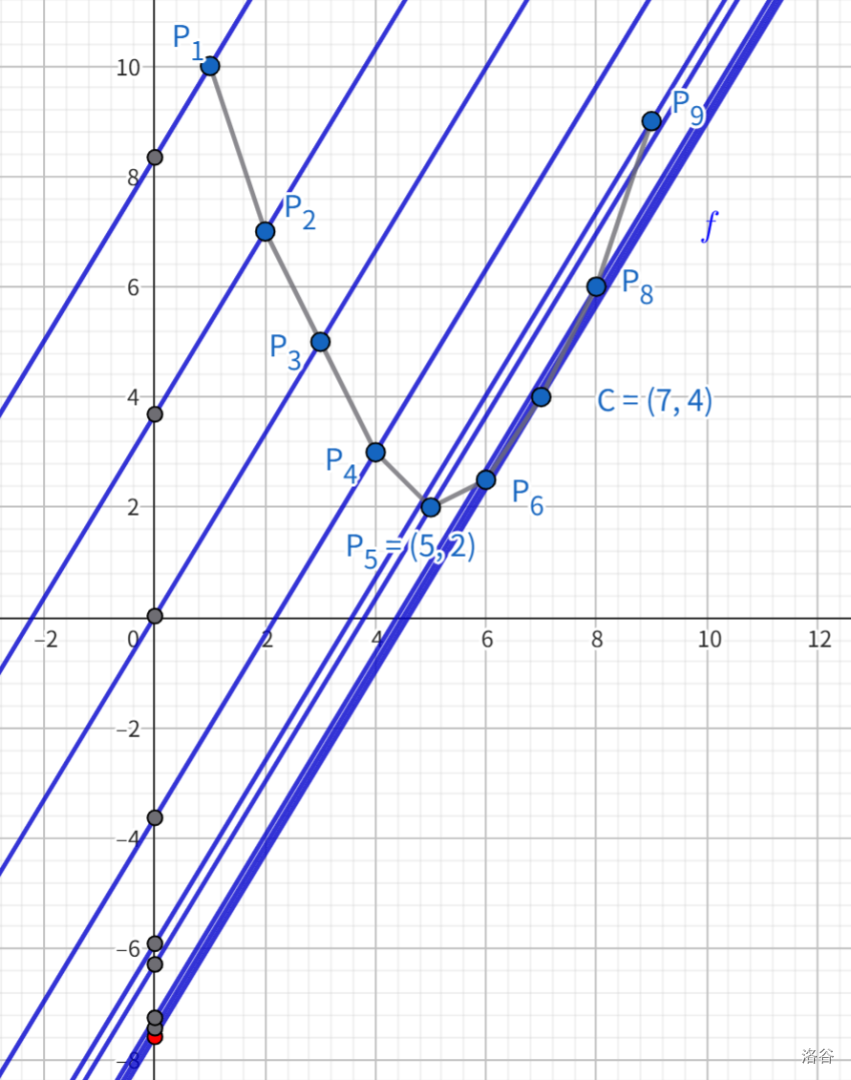
哎,这不跟第一种理解方式中的 \(g(i)=f(i)+ki\) 一模一样吗!所以我们也可以快速 dp 求解这个式子,并同样通过记录上一个状态求出切点横坐标 \(p\)。
最后将二分的结果 \(k\) 和其对应的切点横坐标 \(c\) 和截距 \(b(k)\) 代回 \(f(p)=kp+b(k)\) 即可求出 \(f(c)\)。
4.2. 再论三点共线
返回来从这个角度考虑三点共线的情况。此时找不到 \(c\),考虑 \(c\) 右边可以取到的最接近 \(c\) 的点 \(a\)。由于 \(a\) 在 \(c\) 右边,所以我们二分出切点在 \(a\) 时的最小斜率,这对应的切线 \(l_k\) 即为直线 \(AC\)。
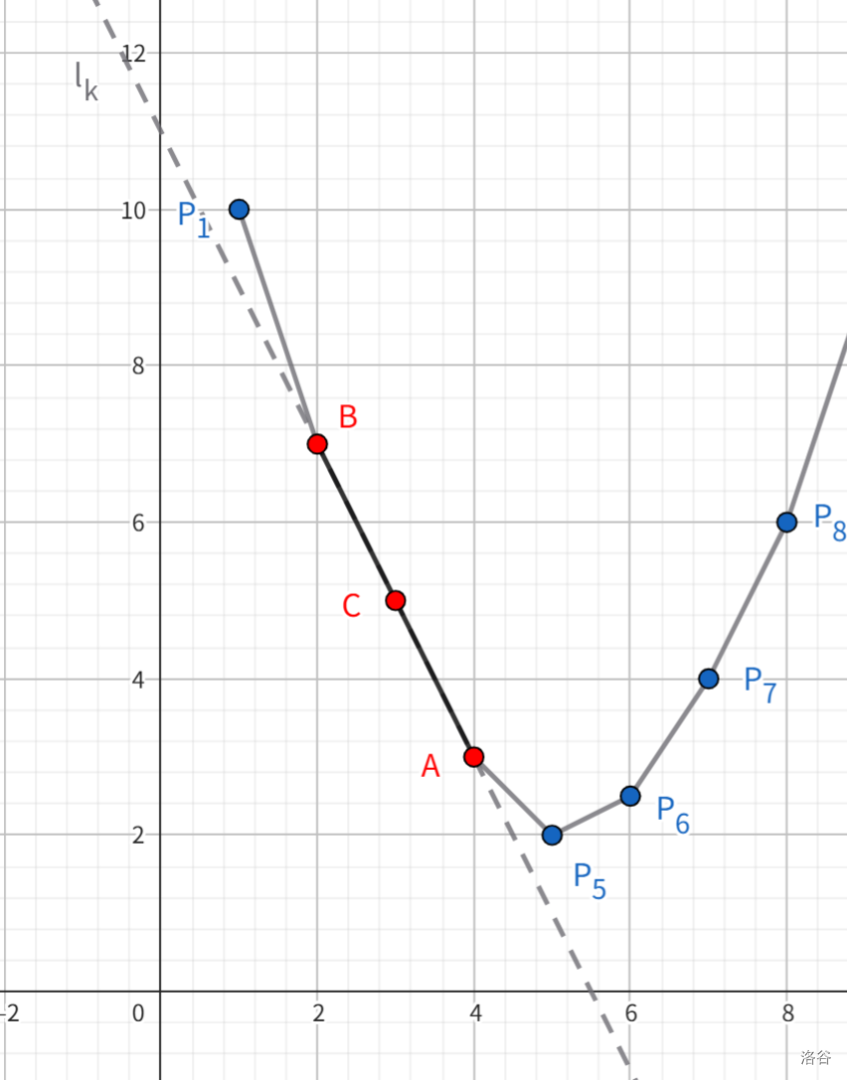
由于过 \(c\),此时的 \(k\) 和 \(b(k)\) 都使用与 \(c\),于是有 \(f(c)=kc+b(k)\)。
4.3. 更多细节
还没讲完,还有细节。
对三点共线情况的研究同样很有启发性。我们说 “二分出切点在 \(a\) 时的最小斜率”,可以发现,当我们二分的 \(k\) 恰为凸壳上相邻两个点的连线的斜率时,
切线
\(\bm{l_k}\)同时切到的时凸壳的一条边而非一个点
,问题就来了:它同时切到了两个(及以上,多点共线时)点,那我们应认为它对应的是哪个切点呢?这关系到我们二分调整范围的过程!这是 wqs 二分最烦容易出错的地方,关键在于要
钦定一个偏序关系
。比如说,前文我们需要 “二分出切点在 \(a\) 时的最小斜率”,我们就可以将这条线的斜率的贡献算到(最)靠右的点内,同时在 dp 值相等时取选择物品个数更大的那个。不管怎样,写二分的时候想好范围如何更新。
另外,大部分题目的 \(f\) 为整数,所以相邻两点连线的斜率/导函数(差分)也为整数,在钦定偏序关系后必然可以二分到整数 \(k\)。对于需要实数二分的题目,由于每个点对应的斜率时一个区间,所以设定好精度,谨防 TLE。
5. 例题
由于笔者涉猎不深,仅能给出一些经典例题了。
- P2619 [国家集训队] Tree I
- P1484 种树
- P5308 [COCI 2018/2019 #4] Akvizna
- P4983 忘情
- P5896 [IOI 2016] aliens
6. 参考资料
- OI Wiki - wqs 二分
- DP 优化方法大杂烩 I. - by qAlex_Weiq
- DP的各种优化(动态规划,决策单调性,斜率优化,带权二分,单调栈,单调队列)- by Flash_Hu


















这一切,似未曾拥有